Ovvero perché non si può avere “la botte piena e la moglie ubriaca”. Forse.
di Alberto Pinto.
Introduzione
Nel mondo dell’audio, l’analisi del contenuto in frequenza di un segnale, il cosiddetto spettro, è fondamentale per comprendere e manipolare i suoni. Che si tratti di musica, voce o effetti sonori, la decomposizione di un segnale nel dominio delle frequenze, come si suol dire, ossia nei suoi “ingredienti” sinusoidali, ci offre una prospettiva dettagliata sulle componenti armoniche e sulle caratteristiche timbriche. Tuttavia, quando visualizziamo lo spettro di un segnale, normalmente stiamo osservando solamente il contenuto frequenziale di una finestra temporale di quel segnale. Questa limitazione temporale introduce un principio fondamentale di indeterminazione, simile al principio di Heisenberg in fisica, che stabilisce una relazione inversa tra risoluzione temporale e frequenziale, ossia tra capacità di vedere il tempo o di vedere le frequenze.
Il principio di indeterminazione di Heisenberg nei segnali
Originariamente formulato nella meccanica quantistica, il principio di indeterminazione di Heisenberg afferma che non è possibile conoscere simultaneamente con precisione arbitraria sia la posizione sia la quantità di moto di una particella, come ad esempio un elettrone. Queste coppie di grandezze che non è possibile conoscere simultaneamente vengono chiamate grandezze coniugate. Nel contesto dell’analisi dei segnali audio (ma vale in generale per qualsiasi segnale), il tempo e la frequenza sono grandezze coniugate: maggiore è la precisione con cui conosciamo quando un certo evento accade nel segnale (ad esempio una nota ben localizzata nel tempo), minore è la precisione con cui possiamo determinarne la frequenza, e viceversa. In altre parole, non possiamo conoscere simultaneamente e con precisione la localizzazione nel tempo e la frequenza di un evento sonoro.
Matematicamente, questo principio può essere espresso attraverso la trasformata di Fourier e le sue proprietà. La trasformata di Fourier permette di passare dal dominio del tempo al dominio della frequenza ma, quando prendiamo solamente una porzione limitata al segnale attraverso un troncamento dello stesso, questo purtroppo causa un allargamento dello spettro misurato, introducendo incertezza. Il troncamento del segnale viene anche chiamato “finestratura” perché viene realizzato moltiplicando, istante di tempo per istante di tempo, il segnale (lungo) che ci interessa tagliare per un altro segnale detto “finestra”, che è sempre nullo tranne in un intervallo di tempo molto breve, dove può assumere le forme più diverse, come vedremo tra poco.
In Fig. 1 si mostra come una sinusoide infinita (grafico in alto a sinistra) abbia uno spettro estremamente definito, addirittura un “impulso” o Delta di Dirac (grafico in alto a destra). Finestrando la sinusoide nel tempo, ossia moltiplicandola per una funzione finestra (nell’esempio una Gaussiana) il relativo spettro si rende più indeterminato. Con una finestra infinitesimamente stretta addirittura lo spettro del segnale diventa una costante, impedendo di fatto il riconoscimento della frequenza della sinusoide.
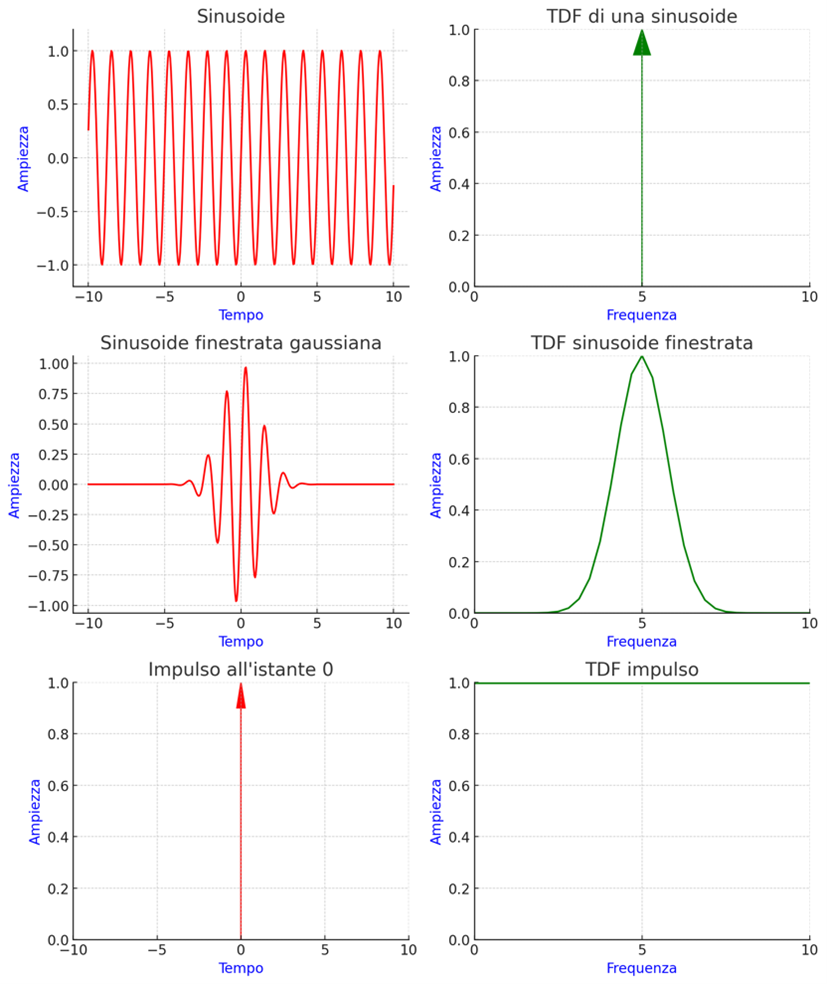
Fig. 1 – Effetto sullo spettro della finestratura di un segnale sinusoidale.
Il Compromesso tra tempo e frequenza
La scelta della dimensione della finestra temporale rappresenta un compromesso fondamentale nell’analisi dei segnali: non possiamo avere simultaneamente alta risoluzione temporale (la famosa botte piena) e alta risoluzione frequenziale (l’altrettanto famosa moglie ubriaca). Ma cosa significano esattamente risoluzione temporale e risoluzione frequenziale?
Risoluzione temporale
La risoluzione temporale si riferisce alla capacità di un sistema di distinguere tra eventi che avvengono in momenti diversi nel tempo. È la minima differenza di tempo tra due eventi che il sistema può rilevare separatamente. Una finestra temporale corta offre alta risoluzione temporale perché è confinata in un breve intervallo di tempo, permettendo di localizzare con precisione quando si verificano specifici eventi o cambiamenti nel segnale.
Risoluzione frequenziale
La risoluzione frequenziale si riferisce alla capacità di distinguere tra componenti di frequenza vicine nel dominio delle frequenze. È la minima differenza di frequenza tra due componenti che possono essere rilevate come separate. Una finestra temporale lunga offre alta risoluzione frequenziale perché contiene più cicli delle onde sinusoidali a diverse frequenze, permettendo di distinguere con maggiore precisione le diverse componenti frequenziali del segnale.
Il compromesso
Secondo il principio di indeterminazione, esiste una relazione inversa tra risoluzione temporale e frequenziale:
- Finestre temporali corte: Offrono alta risoluzione temporale ma bassa risoluzione frequenziale. Ideali per analizzare eventi transitori o rapidi cambiamenti nel segnale, ma non permettono di distinguere accuratamente componenti di frequenza vicine.
- Finestre temporali lunghe: Offrono alta risoluzione frequenziale ma bassa risoluzione temporale. Ideali per analizzare componenti frequenziali stazionarie del segnale, ma non permettono di localizzare con precisione quando queste componenti si verificano nel tempo.
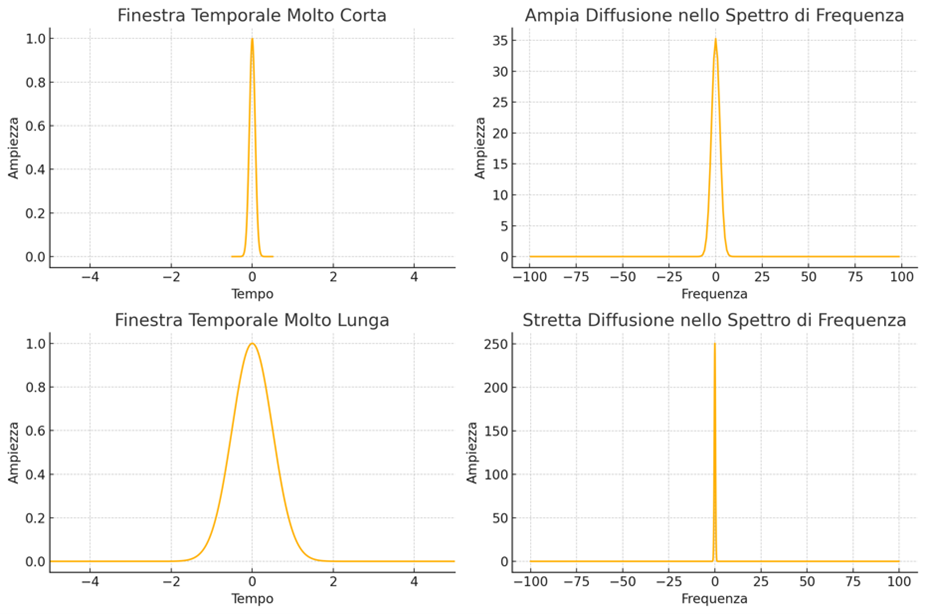
Fig. 2 – Effetto della dimensione della finestra sul leakage spettrale.
In Fig. 2 si mostra come finestre temporali corte causino una maggiore diffusione (leakage) nello spettro rispetto a finestre temporali lunghe.
Tipi di finestre e leakage spettrale
Oltre alla dimensione della finestra, la forma della finestra stessa ha un impatto significativo sull’analisi spettrale. Diversi tipi di finestre (cfr. Fig. 3) vengono utilizzati per minimizzare effetti indesiderati come il leakage spettrale e per ottimizzare il compromesso tra risoluzione temporale e frequenziale.
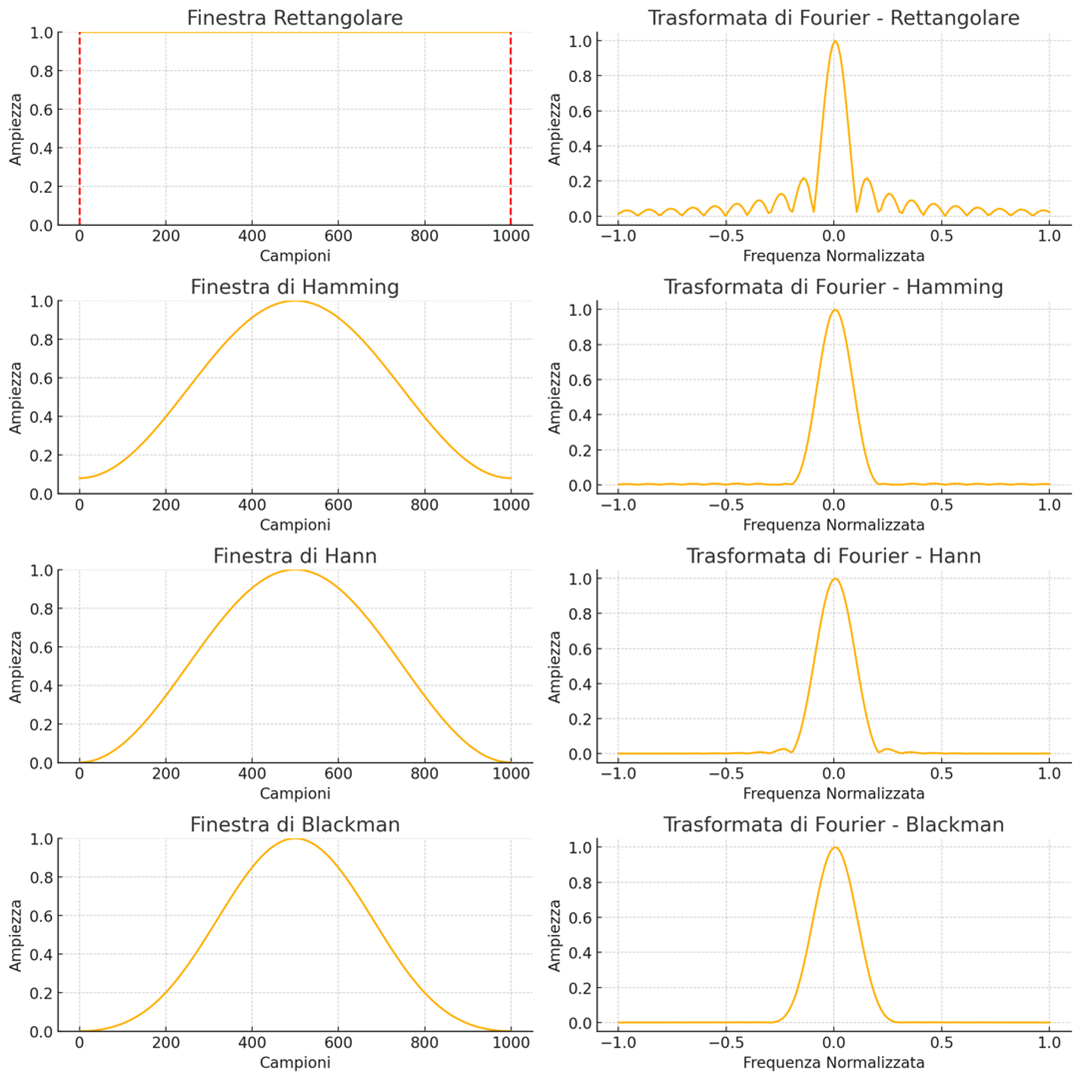
Fig. 3 – Differenti forme di finestre per l’analisi spettrale.
Il leakage spettrale si verifica quando l’energia di una componente frequenziale si “diffonde” su altre frequenze nel dominio spettrale. Questo avviene perché la trasformata di Fourier di un segnale finito (limitato nel tempo) non può rappresentare perfettamente una singola frequenza, ma genera un insieme di frequenze adiacenti. Il leakage spettrale può mascherare o distorcere le reali componenti frequenziali del segnale, rendendo difficile un’analisi accurata.
Perché scegliere una finestra piuttosto che un’altra?
La scelta della forma della finestra dipende dalle esigenze specifiche dell’analisi:
- Riduzione del leakage spettrale: Finestre come Hamming e Blackman riducono il leakage, utile per evitare che l’energia di una frequenza influenzi le frequenze adiacenti.
- Risoluzione frequenziale: Finestre con un lobo principale stretto, come la rettangolare o la Hann, offrono migliore risoluzione frequenziale, permettendo di distinguere componenti di frequenza vicine.
- Attenuazione dei lobi laterali: Finestre con lobi laterali attenuati, come la Blackman, riducono l’impatto delle componenti a frequenze lontane, un fatto utile in segnali con ampia gamma dinamica.
Applicazioni nelle DAW
Strumenti professionali di audio digitale come le DAW (Digital Audio Workstation) o software specifici come iZotope RX offrono all’utente la possibilità di scegliere sia il tipo di finestra che la lunghezza della finestra durante l’analisi spettrale. Questi parametri possono essere impostati per adattare l’analisi alle esigenze specifiche del progetto, bilanciando risoluzione temporale e frequenziale.
In iZotope RX ad esempio (Fig. 4), durante l’utilizzo di strumenti come l’analizzatore di spettro, è possibile:
- Selezionare il tipo di finestra (Window): Scegliere tra diverse finestre (Hamming, Hann, Blackman, ecc.) per ottimizzare l’analisi in base al segnale.
- Impostare la larghezza della finestra (FFT Size): Regolando la durata della finestra, si controlla la risoluzione temporale e frequenziale, adattando l’analisi a segnali transitori o stazionari.
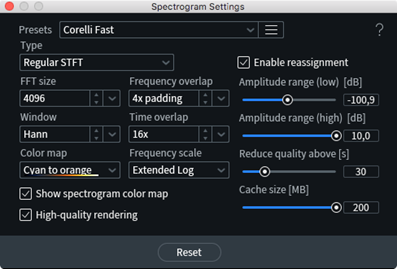
Fig. 4 – Finestra di impostazioni dello spettrogramma di iZotope RX 11.
Supponiamo ad esempio di dover analizzare un segnale musicale contenente due note con frequenze molto vicine.
- Con finestra rettangolare corta: Potremmo non distinguere le due note nello spettro a causa della bassa risoluzione frequenziale e dell’alto leakage spettrale.
- Con finestra di Hamming lunga: Miglioriamo la risoluzione frequenziale e riduciamo il leakage spettrale, permettendo di distinguere le due componenti.
Se il segnale contiene rapidi transitori e siamo interessati a localizzarli nel tempo, una finestra corta con forma rettangolare o Hann potrebbe essere più appropriata, nonostante l’aumento del leakage spettrale, perché privilegia la risoluzione temporale.
Nel contesto dello spettrogramma di iZotope RX 11, le impostazioni di frequency overlap e time overlap giocano un ruolo cruciale nella qualità e nella risoluzione della rappresentazione grafica del segnale audio.
- Time Overlap: Aumentando l’overlap temporale, si sovrappongono più finestre temporali nel calcolo dello spettrogramma. Questo aumenta la risoluzione temporale, permettendo di catturare dettagli più fini dei cambiamenti rapidi del segnale nel tempo. Tuttavia, un overlap troppo alto può aumentare il carico computazionale e ridurre la chiarezza della visualizzazione.
- Frequency Overlap: L’overlap in frequenza consente una maggiore interpolazione tra le bande di frequenza vicine, migliorando la risoluzione frequenziale. Un overlap più elevato aiuta a distinguere frequenze vicine con maggiore precisione, ma potrebbe sfocare i dettagli temporali se non bilanciato correttamente.
In sintesi, un corretto bilanciamento tra frequency e time overlap è essenziale per ottimizzare la risoluzione dello spettrogramma in iZotope RX, migliorando la qualità visiva e informativa dell’analisi audio. Per maggiori informazioni su iZotope RX si rimanda al testo del Prof. Simone Corelli del CESMA citato in bibliografia.
Conclusione
Il principio di indeterminazione di Heisenberg nell’analisi dei segnali audio digitali evidenzia una limitazione fondamentale nella capacità della strumentazione di analizzare simultaneamente il contenuto temporale e frequenziale di un segnale con precisione arbitraria. Comprendere il compromesso tra risoluzione temporale e frequenziale e la scelta appropriata della finestra sono competenze essenziali per chi lavora nel settore audio.
L’utilizzo professionale di software come iZotope RX richiede una conoscenza approfondita di questi concetti, permettendo di sfruttare appieno le capacità del software e di ottenere risultati di alta qualità. La formazione e l’esperienza nel gestire questi parametri fanno la differenza tra un approccio dilettantesco e uno professionale.
Forse
Quanto abbiamo appena esposto è tutto vero, tuttavia sembra esserci una contraddizione tra le limitazioni imposte dal principio di indeterminazione e le straordinarie capacità dell’orecchio umano. Mentre da un punto di vista tecnico ci si deve affidare alle misurazioni spettrali fornite da strumenti software per analizzare e manipolare i suoni, l’orecchio umano è in grado di percepire simultaneamente dettagli temporali e frequenziali con grande precisione. Come si spiega questo fenomeno?
La risposta risiede nella complessità e nell’efficienza del sistema uditivo umano, che utilizza meccanismi biologici avanzati per elaborare i suoni. A differenza degli strumenti digitali, che sono limitati da analisi lineari e stazionarie, l’orecchio umano impiega processi non lineari e adattativi. Le cellule ciliate nella coclea rispondono a specifiche frequenze, mentre le reti neurali nel cervello elaborano informazioni temporali e spaziali. Questo consente di percepire simultaneamente l’intonazione di una nota e il suo attacco, integrando informazioni di tempo e frequenza senza le limitazioni imposte dal principio di indeterminazione.
Per i professionisti dell’audio quindi comprendere questa apparente contraddizione è fondamentale. Sebbene gli strumenti di analisi forniscano dati preziosi e insostituibili, è essenziale ricordare che l’esperienza uditiva umana va oltre ciò che può essere misurato strumentalmente. Pertanto, un approccio professionale richiede di combinare le competenze tecniche con l’ascolto critico, utilizzando sia le misurazioni oggettive sia la propria percezione per ottenere risultati sonori ottimali.
Bibliografia
- Oppenheim, A.V., & Schafer, R.W. (1999). Discrete-Time Signal Processing. Prentice Hall.
- Harris, F.J. (1978). On the use of windows for harmonic analysis with the discrete Fourier transform. Proceedings of the IEEE, 66(1), 51-83.
- Mallat, S. (1999). A Wavelet Tour of Signal Processing. Academic Press.
- Corelli, S. (2023). Radiografare il suono con iZotope RX, seconda edizione, ed CESMA.
