Oder warum man nicht alles gleichzeitig haben kann. Vielleicht.
von Alberto Pinto.
Einführung
In der Welt des Audios ist die Analyse des Frequenzinhalts eines Signals, das sogenannte Spektrum, von grundlegender Bedeutung, um Klänge zu verstehen und zu manipulieren. Ob Musik, Sprache oder Soundeffekte, die Zerlegung eines Signals im Frequenzbereich, wie man so sagt, also in seine sinusförmigen „Bestandteile“, bietet uns eine detaillierte Perspektive auf die harmonischen Komponenten und die klanglichen Eigenschaften. Wenn wir jedoch das Spektrum eines Signals visualisieren, beobachten wir normalerweise nur den Frequenzinhalt eines Zeitfensters dieses Signals. Diese zeitliche Begrenzung führt zu einem grundlegenden Unschärfeprinzip, ähnlich dem Heisenbergschen Prinzip in der Physik, das eine umgekehrte Beziehung zwischen zeitlicher und frequenzieller Auflösung herstellt, d. h. zwischen der Fähigkeit, die Zeit oder die Frequenzen zu sehen.
Das Heisenbergsche Unschärfeprinzip in Signalen
Das ursprünglich in der Quantenmechanik formulierte Heisenbergsche Unschärfeprinzip besagt, dass es unmöglich ist, gleichzeitig sowohl die Position als auch den Impuls eines Teilchens, wie beispielsweise eines Elektrons, mit beliebiger Genauigkeit zu bestimmen. Diese Paare von Größen, die nicht gleichzeitig genau bestimmt werden können, werden als bezeichnet. Im Kontext der Audiosignalanalyse (dies gilt aber allgemein für jedes Signal) sind Zeit und Frequenz konjugierte Größen: Je genauer wir wissen, wann ein bestimmtes Ereignis im Signal auftritt (zum Beispiel eine zeitlich gut lokalisierte Note), desto ungenauer können wir dessen Frequenz bestimmen und umgekehrt. Mit anderen Worten können wir nicht gleichzeitig und präzise die zeitliche Lokalisierung und die Frequenz eines Klangereignisses bestimmen.
Mathematisch lässt sich dieses Prinzip durch die Fourier-Transformation und ihre Eigenschaften ausdrücken. Die Fourier-Transformation ermöglicht den Übergang vom Zeit- in den Frequenzbereich, aber wenn wir nur einen begrenzten Teil des Signals durch eine Trunkierung desselben betrachten, führt dies leider zu einer Verbreiterung des gemessenen Spektrums, wodurch eine Unsicherheit entsteht. Die Trunkierung des Signals wird auch als „Fensterung“ bezeichnet, da sie durch Multiplikation des (langen) Signals, das wir abschneiden möchten, mit einem anderen Signal, dem so genannten „Fenster“, realisiert wird, das immer Null ist, außer in einem sehr kurzen Zeitintervall, wo es die unterschiedlichsten Formen annehmen kann, wie wir gleich sehen werden.
In Abb. 1 wird gezeigt, wie eine unendliche Sinuskurve (Grafik oben links) ein extrem definiertes Spektrum aufweist, sogar einen „Impuls“ oder ein Dirac-Delta (Grafik oben rechts). Durch die Fensterung der Sinuskurve in der Zeit, d. h. durch Multiplikation mit einer Fensterfunktion (im Beispiel eine Gaußsche Funktion), wird das entsprechende Spektrum unbestimmter. Bei einem infinitesimal schmalen Fenster wird sogar das Spektrum des Signals zu einer Konstanten, was die Erkennung der Frequenz der Sinuskurve faktisch verhindert.
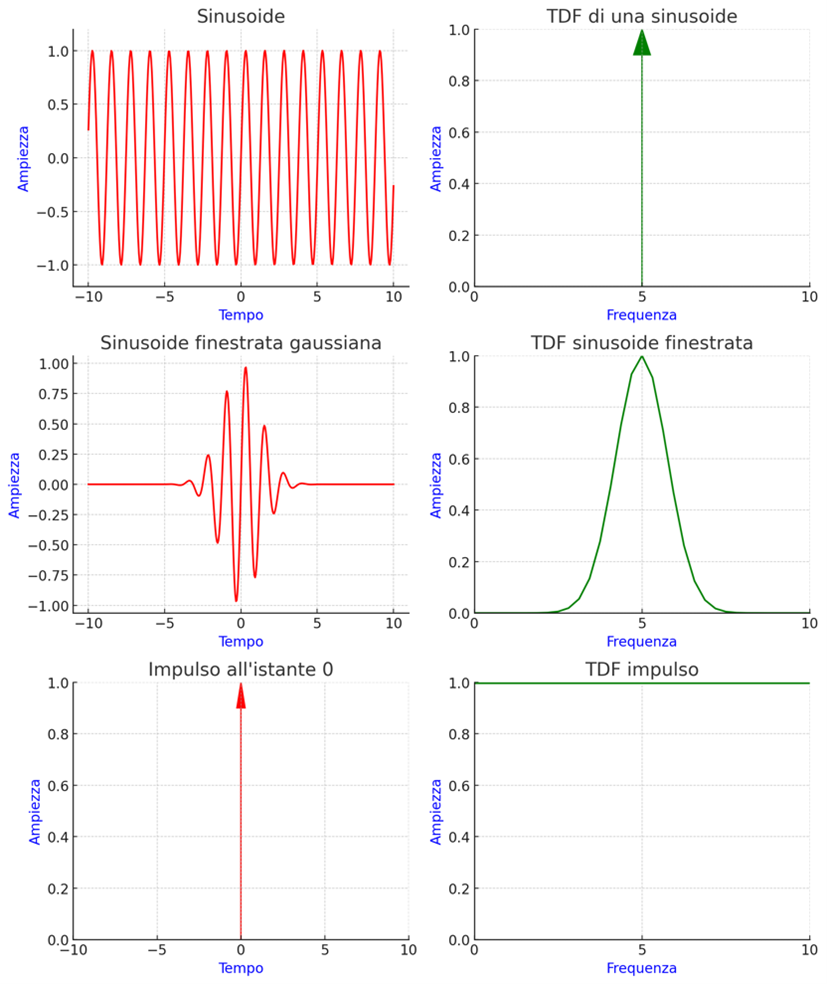
Abb. 1 – Auswirkung der Fensterung auf das Spektrum eines Sinussignals.
Der Kompromiss zwischen Zeit und Frequenz
Die Wahl der Fenstergröße stellt einen fundamentalen Kompromiss in der Signalanalyse dar: Wir können nicht gleichzeitig eine hohe zeitliche Auflösung und eine hohe Frequenzauflösung haben. Aber was bedeuten zeitliche und frequenzielle Auflösung genau?
Zeitliche Auflösung
Die zeitliche Auflösung bezieht sich auf die Fähigkeit eines Systems, zwischen Ereignissen zu unterscheiden, die zu verschiedenen Zeitpunkten auftreten. Es ist der minimale zeitliche Abstand zwischen zwei Ereignissen, den das System getrennt erfassen kann. Ein kurzes Zeitfenster bietet eine hohe zeitliche Auflösung, da es auf ein kurzes Zeitintervall begrenzt ist und es ermöglicht, den genauen Zeitpunkt spezifischer Ereignisse oder Änderungen im Signal zu lokalisieren.
Frequenzauflösung
Die Frequenzauflösung bezieht sich auf die Fähigkeit, zwischen nahe beieinanderliegenden Frequenzkomponenten im Frequenzbereich zu unterscheiden. Es ist der minimale Frequenzunterschied zwischen zwei Komponenten, die noch als getrennt erkannt werden können. Ein langes Zeitfenster bietet eine hohe Frequenzauflösung, da es mehr Zyklen der Sinuswellen verschiedener Frequenzen enthält und damit eine genauere Unterscheidung der verschiedenen Frequenzkomponenten des Signals ermöglicht.
Der Kompromiss
Nach dem Unschärfeprinzip besteht eine inverse Beziehung zwischen zeitlicher und frequenzieller Auflösung:
- Kurze Zeitfenster: Bieten hohe zeitliche Auflösung, aber niedrige Frequenzauflösung. Ideal für die Analyse von transienten Ereignissen oder schnellen Signaländerungen, erlauben aber keine genaue Unterscheidung nahe beieinanderliegender Frequenzkomponenten.
- Lange Zeitfenster: Bieten hohe Frequenzauflösung, aber niedrige zeitliche Auflösung. Ideal für die Analyse stationärer Frequenzkomponenten des Signals, erlauben aber keine präzise zeitliche Lokalisierung dieser Komponenten.
Abb. 2 – Auswirkung der Fenstergröße auf die spektrale Streuung.
In Abb. 2 wird gezeigt, wie kurze Zeitfenster eine stärkere Streuung (Leakage) im Spektrum verursachen als lange Zeitfenster.
Fenstertypen und spektrales Leakage
Neben der Fenstergröße hat auch die Form des Fensters selbst einen signifikanten Einfluss auf die Spektralanalyse. Verschiedene Fenstertypen (vgl. Abb. 3) werden verwendet, um unerwünschte Effekte wie spektrales Leakage zu minimieren und den Kompromiss zwischen zeitlicher und frequenzieller Auflösung zu optimieren.
Abb. 3 – Verschiedene Fensterformen für die Spektralanalyse.
Die Spektrale Leckage tritt auf, wenn die Energie einer Frequenzkomponente auf andere Frequenzen im Spektralbereich „verschmiert“ wird. Dies geschieht, weil die Fourier-Transformation eines endlichen (zeitlich begrenzten) Signals nicht perfekt eine einzelne Frequenz darstellen kann, sondern eine Menge benachbarter Frequenzen erzeugt. Die spektrale Leckage kann die realen Frequenzkomponenten des Signals maskieren oder verzerren, was eine genaue Analyse erschwert.
Warum ein Fenster statt eines anderen wählen?
Die Wahl der Fensterform hängt von den spezifischen Analyseanforderungen ab:
- Reduzierung des spektralen Leakage: Fenster wie Hamming und Blackman reduzieren das Leakage, was nützlich ist, um zu verhindern, dass die Energie einer Frequenz benachbarte Frequenzen beeinflusst.
- Frequenzauflösung: Fenster mit einer schmalen Hauptkeule, wie das rechteckige oder das Hann-Fenster, bieten bessere Frequenzauflösung und ermöglichen die Unterscheidung nahe beieinanderliegender Frequenzkomponenten.
- Dämpfung der Nebenkeulen: Fenster mit gedämpften Nebenkeulen, wie das Blackman-Fenster, reduzieren den Einfluss weit entfernter Frequenzkomponenten, was bei Signalen mit großem Dynamikbereich nützlich ist.
Anwendungen in DAWs
Professionelle Digital-Audio-Werkzeuge wie DAWs (Digital Audio Workstation) oder spezielle Software wie iZotope RX bieten dem Benutzer die Möglichkeit, sowohl den Fenstertyp als auch die Fensterlänge während der Spektralanalyse zu wählen. Diese Parameter können angepasst werden, um die Analyse an die spezifischen Projektanforderungen anzupassen und die zeitliche und frequenzielle Auflösung auszubalancieren.
In iZotope RX zum Beispiel (Abb. 4) ist es bei der Verwendung von Werkzeugen wie dem Spektrumanalysator möglich:
- Den Fenstertyp (Window) zu wählen: Auswahl zwischen verschiedenen Fenstern (Hamming, Hann, Blackman, etc.) zur Optimierung der Analyse basierend auf dem Signal.
- Die Fensterbreite (FFT Size) einzustellen: Durch Anpassung der Fensterdauer wird die zeitliche und frequenzielle Auflösung gesteuert, wodurch die Analyse an transiente oder stationäre Signale angepasst werden kann.
Abb. 4 – Einstellungsfenster des Spektrogramms von iZotope RX 11.
Nehmen wir zum Beispiel an, wir müssen ein Musiksignal analysieren, das zwei Noten mit sehr ähnlichen Frequenzen enthält.
- Mit kurzem Rechteckfenster: Wir könnten die beiden Noten im Spektrum aufgrund der niedrigen Frequenzauflösung und des hohen spektralen Leakage nicht unterscheiden.
- Mit langem Hamming-Fenster: Wir verbessern die Frequenzauflösung und reduzieren das spektrale Leakage, wodurch die beiden Komponenten unterschieden werden können.
Wenn das Signal schnelle Transienten enthält und wir daran interessiert sind, diese zeitlich zu lokalisieren, könnte ein kurzes Fenster mit rechteckiger oder Hann-Form trotz des erhöhten spektralen Leakage geeigneter sein, da es die zeitliche Auflösung bevorzugt.
Im Kontext des Spektrogramms von iZotope RX 11 spielen die Einstellungen für frequency overlap und time overlap eine entscheidende Rolle für die Qualität und Auflösung der grafischen Darstellung des Audiosignals.
- Time Overlap: Durch Erhöhung der zeitlichen Überlappung werden mehr Zeitfenster bei der Berechnung des Spektrogramms überlagert. Dies erhöht die zeitliche Auflösung und ermöglicht es, feinere Details schneller Signaländerungen in der Zeit zu erfassen. Eine zu hohe Überlappung kann jedoch die Rechenbelastung erhöhen und die Klarheit der Darstellung reduzieren.
- Frequency Overlap: Die Frequenzüberlappung ermöglicht eine bessere Interpolation zwischen benachbarten Frequenzbändern und verbessert die Frequenzauflösung. Eine höhere Überlappung hilft, nahe beieinanderliegende Frequenzen genauer zu unterscheiden, kann aber die zeitlichen Details verwischen, wenn sie nicht richtig ausbalanciert ist.
Zusammenfassend ist eine korrekte Balance zwischen Frequency und Time Overlap wesentlich für die Optimierung der Spektrogrammauflösung in iZotope RX und verbessert die visuelle und informative Qualität der Audioanalyse. Für weitere Informationen zu iZotope RX wird auf den Text von Prof. Simone Corelli des CESMA in der Bibliografie verwiesen.
Fazit
Das Heisenbergsche Unschärfeprinzip in der digitalen Audiosignalanalyse zeigt eine fundamentale Einschränkung in der Fähigkeit der Instrumente, den zeitlichen und frequenziellen Inhalt eines Signals gleichzeitig mit beliebiger Genauigkeit zu analysieren. Das Verständnis des Kompromisses zwischen zeitlicher und frequenzieller Auflösung sowie die angemessene Fensterwahl sind wesentliche Kompetenzen für jeden, der im Audiobereich arbeitet.
Die professionelle Nutzung von Software wie iZotope RX erfordert ein tiefgehendes Verständnis dieser Konzepte, um die Fähigkeiten der Software voll auszuschöpfen und qualitativ hochwertige Ergebnisse zu erzielen. Ausbildung und Erfahrung im Umgang mit diesen Parametern machen den Unterschied zwischen einem amateurhaften und einem professionellen Ansatz.
Vielleicht
Was wir gerade dargelegt haben, ist alles wahr, dennoch scheint es einen Widerspruch zwischen den durch das Unschärfeprinzip auferlegten Beschränkungen und den außergewöhnlichen Fähigkeiten des menschlichen Gehörs zu geben. Während man sich aus technischer Sicht auf die von Software-Werkzeugen bereitgestellten Spektralmessungen verlassen muss, um Klänge zu analysieren und zu manipulieren, ist das menschliche Ohr in der Lage, zeitliche und frequenzielle Details gleichzeitig mit großer Präzision wahrzunehmen. Wie lässt sich dieses Phänomen erklären?
Die Antwort liegt in der Komplexität und Effizienz des menschlichen Hörsystems, das fortgeschrittene biologische Mechanismen zur Klangverarbeitung nutzt. Im Gegensatz zu digitalen Instrumenten, die durch lineare und stationäre Analysen begrenzt sind, verwendet das menschliche Ohr nichtlineare und adaptive Prozesse. Die Haarzellen in der Cochlea reagieren auf spezifische Frequenzen, während neuronale Netze im Gehirn zeitliche und räumliche Informationen verarbeiten. Dies ermöglicht es, gleichzeitig die Tonhöhe einer Note und ihren Einsatz wahrzunehmen, wobei Zeit- und Frequenzinformationen ohne die durch das Unschärfeprinzip auferlegten Beschränkungen integriert werden.
Für Audioprofis ist das Verständnis dieses scheinbaren Widerspruchs daher fundamental. Obwohl Analysewerkzeuge wertvolle und unersetzliche Daten liefern, ist es wichtig zu bedenken, dass die menschliche Hörerfahrung über das instrumentell Messbare hinausgeht. Daher erfordert ein professioneller Ansatz die Kombination von technischen Fähigkeiten mit kritischem Hören, wobei sowohl objektive Messungen als auch die eigene Wahrnehmung genutzt werden, um optimale Klangergebnisse zu erzielen.
Bibliografie
- Oppenheim, A.V., & Schafer, R.W. (1999). Discrete-Time Signal Processing. Prentice Hall.
- Harris, F.J. (1978). On the use of windows for harmonic analysis with the discrete Fourier transform. Proceedings of the IEEE, 66(1), 51-83.
- Mallat, S. (1999). A Wavelet Tour of Signal Processing. Academic Press.
- Corelli, S. (2023). Radiografare il suono con iZotope RX, zweite Auflage, ed CESMA.